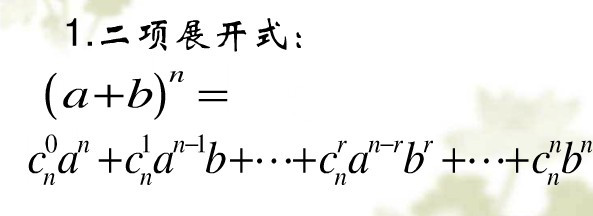半夜睡不着，胡思乱想，开始想起高中老师教过的计算以整数最后一位是5的计算小技巧，如5*5，15*15，25*25，于是就想这样我来脑算下255*255。

老师当时教的计算方法如下：

5*5 = （1*2)5=25
15*15=(1*2)(5*5)=225
25*25=(2*3)(5*5)=625
35*35=(3*4)(5*5)=1225
45*45=(4*5)(5*5)=2025
55*55=(5*6)(5*5)=3025
....
255*255=(2*3)(55*55)=63025
255*255=(25*26)(5*5)=(25*25+25)(25)=(630)(25)=63025

...
其实我是想算256^2 = 256*256= ?
(a+b)^2 = a^2+2ab+b^2
其中a = 255,b=1
(a+1)^2 = a^2+2a+1 = 255^2+255^2 +1 = 63025+511+1=63536

这样就算出了2的16次方结果65536，那2的32次方呢？数据库中常用int4来表示id，那支持的范围也可以大概算一下，先算65535的，因为有上面的方法，这个数的开头可能是6*7=42，后面几位数5535*5535，又可以按上面方法继续拆，于是在不考虑累加进位的情况，可大致计算如下：

65535^2>(6*7)(5*6)(5*6)(3*4)(5*5)=4230301225
65536^2 肯定超过42亿